Käytännössä eri vertaustähdistä lasketuissa nollapisteissä on usein eroja johtuen siitä, että niiden värit eivät ole samat. Yleensä onkin parempi käyttää tarkempaa kaavaa
    zp_i = m_i(oikea) – m(mitattu) – l(B – V)_i
missä zp_i on tähdestä i laskettu nollapiste, l on käytetyn laitteen värikerroin ja (B – V)_i tähden väri. NOT-teleskoopin ALFOSC-mittalaitteelle l = –0.04. Tähdille käytämme tunnettuja (B – V)_i-arvoja, tässä tapauksessa (B – V)_B = 0.96 ja (B – V)_C2 = 1.00. Näinollen saamme kahdelle tähdellemme nollapisteet:
    zp_B  = 14.77 – 14.060 – (–0.05) × 0.96 = 0.758
    zp_C2 = 14.18 – 13.455 – (–0.05) × 1.00 = 0.775
Kun yksittäiset nollapisteet on laskettu, lasketaan kuvan nollapiste zp_av ottamalla keskiarvo yksittäisistä arvoista. Tässä tapauksessa zp_av = 0.767. Kohteen korjattu magnitudi saadaan tämän jälkeen yhtälöstä
    m_obj = m_obj(mitattu) + zp_av + l(B – V)_obj
BL Lac -kohteille voidaan yleisesti käyttää arviota (B – V)_i = 0.5. Siten kohteen 3C 66A kirkkaudeksi saadaan
    m_{3C 66A} = 13.902 + 0.767 + (–0.05) × 0.5 = 14.694

2.5 Virherajojen arvioiminen

Kohteen magnitudiin vaikuttavat hyvin monet tekijät ja onkin lähes mahdotonta arvioida täydellisesti niiden aiheuttamia virheitä. Suurimpien virhetekijöiden vaikutus voidaan kuitenkin arvioida ja siten saadaan hyvä arvio kokonaisvirheestä. Suurimmat virhelähteet ovat kohteen mittauksen virhe (s_fot) ja nollapisteen virhe (s_zp).

IRAF:in antama magnitudin virheraja on jokseenkin sama kuin mittausvirhe s_fot. Nollapisteen virhe s_zp arvioidaan vertaustähtien mittauksista. Mikäli vertaustähtiä on vain yksi on s_zp sama kuin s_fot. Mikäli vertaustähtiä on useampi kuin yksi, on s_zp yhtä kuin nollapisteen zp_av keskiarvon keskivirhe, jonka laskukaava on:

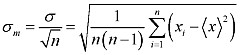
Kaavassa <x> on n havainnosta x_i laskettu keskiarvo. Tässä s_m = s_zp.

Lasketaan esimerkkimme keskiarvon keskivirhe:
    s_zp = ((2 × (2 – 1))^(–1) × ((0.758 – 0.767)² + (0.775 – 0.767)²))^0.5
        = (0.5 × (0.000081 + 0.000064))^0.5 = 0.0085

Kokonaisvirhe voidaan laskea kaavasta

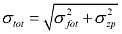
Saamme esimerkissämme siten
    s_tot = (0.040² + 0.009²)^0.5 = 0.041

Lopputulos kannattaa pyöristää lähimpään sadasosaan. Kohteen magnitudi pyöristetään normaalisti matematiikan sääntöjen mukaan, mutta virheraja pyöristetään virheen määritelmän ja luonteen johdosta aina ylöspäin. Näinollen lopputuloksemme on m_3C 66A = 14.69 ± 0.05.